From social media, to sports, to books and everything in between, almost anything can be compared these days. Of course, comparisons can be good or bad, healthy or unhealthy, incredibly insightful or harmful and misleading. This is all true in research as well; however, there’s no escaping that comparisons are a central component of data analysis, so it’s important to know how to make them correctly. In this post we are going to explore percentiles, which are one of the most universally understood ways to draw comparisons from a data set. We will then use percentiles to compare Colorado public library data to data from across the nation and finally, visualize the spread of this data in a box and whisker plot.
What’s a Percentile?
Percentiles are a way to measure how a value compares to all the other values in a data set. To calculate percentiles a data set must be made up of or transformed into quantitative data that can be ordered from the smallest to largest value. Regardless of how many total numbers are in a data set, all the data points will have a percentile rank ranging from 0 to 100 which indicates where the point falls in relation to all other values in that data set. A value’s percentile tells us the percent of values in the data set that are less than or equal to that particular value. The closer a data point is to the minimum value in the set the closer its percentile will be to 0, and the closer a data point is to the maximum value in the set the closer its percentile will be to 100. For example, if a value is in the 75th percentile, that means that 75% of the values in that data set are equal to or lower than this value. Likewise, if a child is in the 90th percentile for height that means that they are taller than 90% of children their age.
State Percentiles for Public Libraries
Before moving forward, let’s ground this explanation of percentiles in some real world public library data. The Institute of Museum and Library Services (IMLS) compiles all the data from the Public Library Surveys (PLS) across the nation, making it possible to find Colorado’s percentile rank for multiple pieces of public library data. By using the 2021 data from the IMLS PLS benchmarking tables and Excel’s percentile rank formula I found that, when compared to all 50 states and the District of Columbia, Colorado ranks above the 85th percentile for the following measures: Circulation per capita (96th percentile), Registered users per capita (96th percentile), Revenue per capita (92nd percentile), and Expenditures per capita (86th percentile). The full data set is included in a table at the end of this post.
So, what do these percentile ranks tell us? These percentiles paint a positive picture of Colorado public library usage because Colorado has more registered library users per capita and material circulation per capita than 96% of states. Revenue and expenditures are also high in comparison to the rest of the nation which shows that Colorado public libraries are, in general, bringing in more money per capita, spending more money per capita, serving more people per capita, and circulating more materials per capita than most other states. In other words, Colorado public libraries are very busy!
One-sided Stories
These findings give Colorado public libraries a lot to celebrate! Before we get too carried away, however, it’s important to note that percentile ranks often only show a small snapshot of a larger story. Percentile ranks on their own, like I’ve shared above, only tell us how a data point compares to the rest of the data set, so there’s a lot of information missing. Not only do percentiles hide the exact values of these data points for Colorado and all other states, we also don’t have any sense of how spread out the data is. All the data points may be clustered together, there could be extreme outliers, or an even distribution. Though we now know where Colorado stands in comparison to other states, we are left in the dark about how close the other data points are to Colorado’s. If many states have a similar value, a small change in Colorado’s number could result in a large difference in percentile rank from year to year. This is why it can be helpful to also visualize the spread of the data when working with percentiles, and we can do this by dividing the data points into quartiles.
So, What’s a Quartile?
Quartiles divide a data set into four groups with the same amount of data points in each group. As stated earlier, percentiles fall from 0 to 100 so quartile one is set at the 25th percentile, quartile two is the 50th percentile, and quartile three is the 75th percentile. This creates four groups of data with the same number of data points in each group: The minimum value to the first quartile, the first quartile to the second quartile, the second quartile to the third quartile, and the third quartile to the maximum value in the data set. The second quartile, or 50th percentile, is also the same as the median, meaning that there are the same number of values that fall below and above it in the data set. Visualizing these quartiles can help us learn more about the spread of the data.
Box and Whisker Plots
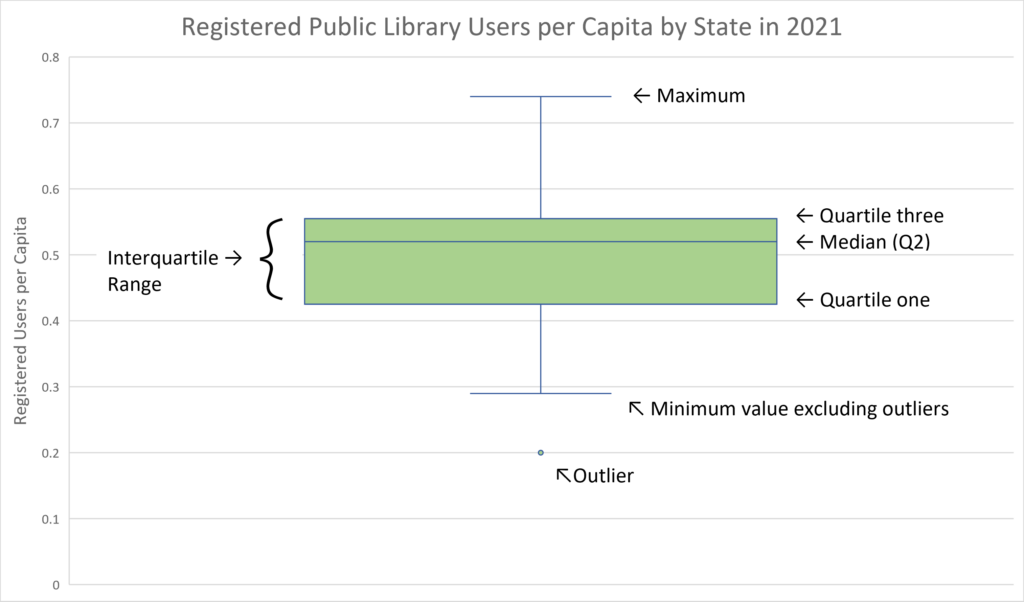
Above is a box and whisker plot of the registered public library users per capita in the U.S. for all 50 states and the District of Columbia created in Excel. The top line in the chart indicates the maximum value in this data set that is not an outlier (0.74). The top border of the box is placed at the 75th percentile, or quartile three (0.56). The line going through the box is the median or 50th percentile (0.52). The bottom border of the box is the value that marks the 25th percentile, or quartile one (0.43), and the bottom line marks the minimum value in the data set that is not an outlier (0.29). The “box” in a box and whisker plot encompasses all the values that fall within the interquartile range of a data set, or in other words between the 1st and 3rd quartile, or the 25th and 75th percentile. This means that the box encompasses the middle half of all values in a data set because half of the data set will always fall into this interquartile range. One quarter of the data set will fall above the interquartile range and one quarter will fall below.
Outliers
Outliers in the data are shown with dots beyond the minimum and maximum lines on a box and whisker plot. They are still a part of the data set, but they fall so far from most of the data that they are indicated separately. Comparing data using percentiles helps reduce the impact that outliers can have on your findings. In the chart above, there is only one outlier–the minimum value 0.20. In this data set, a number must be below 0.24 to be considered an outlier. Excel determines this to be an outlier by using the formula below:
1st Quartile – ((3rd Quartile – 1st Quartile) x 1.5)
0.43 – ((0.56-0.43) x 1.5) = 0.24
Because the minimum value (0.20) in this data set is below 0.24 it is considered an outlier and indicated as a separate dot on this box and whisker plot. This is why the bottom line is set at the second lowest value in this data set which is 0.29.
There aren’t any outliers at the upper end of this data set, but there would be if the data set consisted of any values that were over 0.76. A similar formula is used to determine this:
3rd Quartile + ((3rd Quartile – 1st Quartile) x 1.5)
0.56 – ((0.56-0.43) x 1.5) = 0.76
The maximum value in this data set (0.74) is below 0.76, so it is not considered an outlier. Identifying outliers by creating a box and whisker plot is one method of quickly visualizing how many outliers are in a data set and where they land in comparison to the rest of the data.
Interpreting the Results
Box and whisker plots may also include individual data points along the “whisker” line of the plot. I chose not to include the individual data points in this chart because the data points are closely clustered together with multiple states having the same number of registered users per capita. The main goal of this box and whisker plot is to show how percentiles can be split into quartiles, which help us better understand the spread of this entire data set. This box and whisker plot shows us that this data set is fairly packed together with only one outlier, so including individual data points would only serve to crowd this chart.
To recap, the maximum value in this data set is 0.74 registered users per capita (New Mexico). This means that in New Mexico roughly 74 out of every 100 people have library cards! The minimum value in this data set is 0.2 registered users per capita (Virginia) which is considered an outlier. The 1st quartile falls at 0.43 (New Jersey and Indiana), which means that 25% of states have below 0.43 registered users per capita. The median falls at 0.52 (Texas, Alabama, Florida, and Mississippi), which means that 50% of states have below 0.52 registered users per capita. Approximately a quarter of states have between 0.52 and 0.56 registered users per capita. This is a very small range so we know that many data points are clustered close together to make up this 3rd quartile. The final quarter of states have between .56 and .74 registered users per capita, indicating that the data points are more spread out in this upper quartile.
With 0.66 registered users per capita, Colorado lands between the third quartile and the maximum value, at the 96th percentile to be exact. What this box and whisker plot does not show us is that Colorado actually had the 3rd highest number of registered users per capita in 2021, with only Ohio and New Mexico having more. If this was a larger data set, it would be easier to share a percentile than the exact placement of a single data point within the entire data set. Percentiles are only one of many methods for making comparisons within a data set. While they are commonly used and widely understood by the general public, they give only a limited view of the data. Please see the table below for the full data set I used to make these comparisons. I’m looking forward to exploring some additional methods for data analysis in future Public Library Blueprint posts!
LRS’s Colorado Public Library Data Users Group (DUG) mailing list provides instructions on data analysis and visualization, LRS news, and PLAR updates. To receive posts via email, please complete this form.
| State | Total Circulation per Capita | Percent Rank Circulation | Registered Users per Capita | Percent Rank Registered Users | Revenue per Capita | Percent Rank Revenue per Capita | Expenditures per Capita | Percent Rank Expenditures per Capita |
|---|---|---|---|---|---|---|---|---|
| Alabama | 3.64 | 22% | 0.52 | 50% | 24.22 | 8% | 22.18 | 10% |
| Alaska | 4.31 | 42% | 0.53 | 58% | 63.81 | 82% | 56.29 | 80% |
| Arizona | 3.84 | 28% | 0.41 | 20% | 30.58 | 18% | 27.31 | 16% |
| Arkansas | 4.33 | 44% | 0.59 | 80% | 36.3 | 32% | 31.02 | 24% |
| California | 3.33 | 12% | 0.55 | 72% | 46.78 | 54% | 42.27 | 54% |
| Colorado | 9.07 | 96% | 0.66 | 96% | 76.99 | 92% | 60.48 | 86% |
| Connecticut | 4.65 | 50% | 0.4 | 14% | 62.55 | 80% | 63.81 | 92% |
| Delaware | 2.81 | 8% | 0.29 | 2% | 32.57 | 20% | 31.91 | 32% |
| District of Columbia | 7.53 | 84% | 0.48 | 36% | 98.31 | 100% | 98.42 | 100% |
| Florida | 3.51 | 20% | 0.52 | 50% | 32.58 | 22% | 29.41 | 20% |
| Georgia | 2.28 | 2% | 0.4 | 14% | 20.22 | 2% | 19.63 | 2% |
| Hawaii | 2.59 | 6% | 0.64 | 94% | 25.71 | 12% | 26.04 | 14% |
| Idaho | 8.1 | 90% | 0.49 | 40% | 44.34 | 46% | 39.42 | 46% |
| Illinois | 6.64 | 72% | 0.37 | 8% | 79.05 | 94% | 67.72 | 96% |
| Indiana | 7.47 | 82% | 0.43 | 26% | 70.08 | 90% | 58.55 | 82% |
| Iowa | 5.54 | 64% | 0.61 | 88% | 46.62 | 52% | 44.46 | 58% |
| Kansas | 8.01 | 88% | 0.62 | 90% | 65.21 | 84% | 58.91 | 84% |
| Kentucky | 4.11 | 34% | 0.54 | 66% | 49.07 | 62% | 36.41 | 40% |
| Louisiana | 3.83 | 26% | 0.53 | 58% | 61.54 | 78% | 49.06 | 66% |
| Maine | 4.39 | 46% | 0.53 | 58% | 47.03 | 56% | 44.49 | 60% |
| Maryland | 5.62 | 68% | 0.54 | 66% | 55 | 70% | 49.99 | 72% |
| Massachusetts | 5.5 | 62% | 0.54 | 66% | 51.98 | 66% | 50.95 | 74% |
| Michigan | 5.11 | 54% | 0.42 | 22% | 48.64 | 58% | 41.35 | 52% |
| Minnesota | 7.58 | 86% | 0.59 | 80% | 41.13 | 40% | 39.01 | 44% |
| Mississippi | 1.48 | 0% | 0.52 | 50% | 16.93 | 0% | 15.76 | 0% |
| Missouri | 7.32 | 80% | 0.6 | 86% | 59.04 | 74% | 49.63 | 68% |
| Montana | 4.23 | 38% | 0.4 | 14% | 33.74 | 28% | 31.16 | 26% |
| Nebraska | 7.21 | 78% | 0.63 | 92% | 43.5 | 42% | 39.47 | 48% |
| Nevada | 3.93 | 32% | 0.39 | 12% | 37.34 | 36% | 31.63 | 28% |
| New Hampshire | 5.21 | 56% | 0.49 | 40% | 51.98 | 66% | 49.98 | 70% |
| New Jersey | 4.61 | 48% | 0.43 | 26% | 59.83 | 76% | 53.73 | 78% |
| New Mexico | 4.27 | 40% | 0.74 | 100% | 35.44 | 30% | 31.87 | 30% |
| New York | 3.85 | 30% | 0.5 | 44% | 81.35 | 96% | 69.71 | 98% |
| North Carolina | 3.37 | 16% | 0.55 | 72% | 26.43 | 14% | 23.1 | 12% |
| North Dakota | 4.19 | 36% | 0.35 | 6% | 33.25 | 24% | 31.93 | 34% |
| Ohio | 11.41 | 100% | 0.67 | 98% | 86.39 | 98% | 65.32 | 94% |
| Oklahoma | 5.58 | 66% | 0.56 | 76% | 44.17 | 44% | 38.25 | 42% |
| Oregon | 8.8 | 94% | 0.5 | 44% | 69.8 | 88% | 60.93 | 90% |
| Pennsylvania | 3.74 | 24% | 0.38 | 10% | 27.5 | 16% | 28.06 | 18% |
| Rhode Island | 4.86 | 52% | 0.3 | 4% | 51.67 | 64% | 48.38 | 64% |
| South Carolina | 3.46 | 18% | 0.46 | 32% | 33.43 | 26% | 30.9 | 22% |
| South Dakota | 6.36 | 70% | 0.42 | 22% | 38.17 | 38% | 36.28 | 38% |
| Tennessee | 3.18 | 10% | 0.45 | 30% | 20.89 | 4% | 19.96 | 4% |
| Texas | 3.34 | 14% | 0.52 | 50% | 22.78 | 6% | 21.9 | 8% |
| Utah | 9.98 | 98% | 0.53 | 58% | 44.38 | 48% | 40.58 | 50% |
| Vermont | 5.21 | 56% | 0.51 | 48% | 48.77 | 60% | 46.93 | 62% |
| Virginia | 5.3 | 60% | 0.2 | 0% | 36.62 | 34% | 35.82 | 36% |
| Washington | 8.41 | 92% | 0.47 | 34% | 67.79 | 86% | 60.6 | 88% |
| West Virginia | 2.28 | 2% | 0.56 | 76% | 24.46 | 10% | 20.11 | 6% |
| Wisconsin | 6.97 | 76% | 0.48 | 36% | 46.48 | 50% | 42.3 | 56% |
| Wyoming | 6.73 | 74% | 0.59 | 80% | 57.47 | 72% | 53.28 | 76% |